New Study Claims Black Holes Are Mathematically Impossible

The question: Do black holes exist? is a more nuanced one than you might think. Most people, when they hear this question, interpret it to mean this: do stars really sometimes collapse in a huge stellar explosion, falling inward to become a much smaller, much denser object that does not radiate appreciable light of its own? The answer is, almost certainly, yes.
When physicists and astronomers ask this question, though, they mean it slightly differently: Is there such a thing as an object, regardless of its origin, which has all the properties assigned to a classical black hole? More and more, the answer seems to be no. Stephen Hawking himself, the co-father of black holes and the most famous personality in theoretical physics, has come out to express doubt about that old-school conception of a super-massive star-corpse. Still, there was always at least that first, basic point of agreement: stars do explode and, if big enough, collapse forming something rather like a black hole. Right?
Well, now new research from University of North Carolina may be calling even that into question. Two papers published by a single team earlier this month in ArXiv and ScienceDirect (thus far without peer review), claim that a long-known aspect of a black hole’s formation can be used to prove mathematically that… they don’t form.
Stephen Hawking’s famous insight from 1975 was that black holes give off radiation (now called Hawking radiation) as they form, and this new paper claims to prove that this radiation is in fact converted mass from the star itself. More than that, the papers argue that the exact amount of mass lost to this energy release makes it impossible for a black hole to form. Specifically, a black hole’s violent formation is in fact so violent that it throws out too much of its own mass, lowering the density of the still-forming singularity and ending the collapse, mid-collapse.
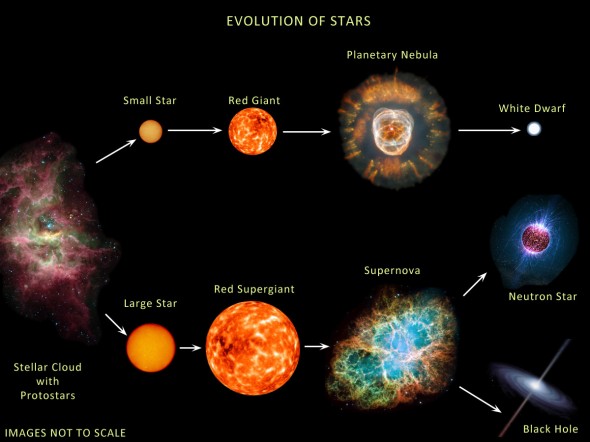
This has enormous implications for a wide variety of areas within physics. Obviously black hole, star, and supernova scientists will be interested in these findings, but don’t forget that a similar density-dependent singularity is supposed to have started the universe itself. If a black hole can’t form then, for the exact same reasons, the Big Bang could not have played out as a classical singularity — and if that’s true then there are going to be a whole lot of physicists struggling to reorient their research, and amend their prior publications.
So, is it true? Well, nobody knows just yet, but in all likelihood this paper is like most seemingly definitive mathematical arguments in astronomical physics, in that it is technically correct but undercut by some glaring physical loophole. The math on display here does prove, solidly, that black holes can’t form given certain assumptions about how they form, meaning that perhaps they don’t form precisely according to those assumptions. There are a wealth of direct observations telling physicists that, for instance, there’s a super-massive black hole (or something very much like our idea of such an object) at the center of many galaxies; all the mathematical logic in the world won’t undo that empirical data, just make the data harder and harder to usefully understand.
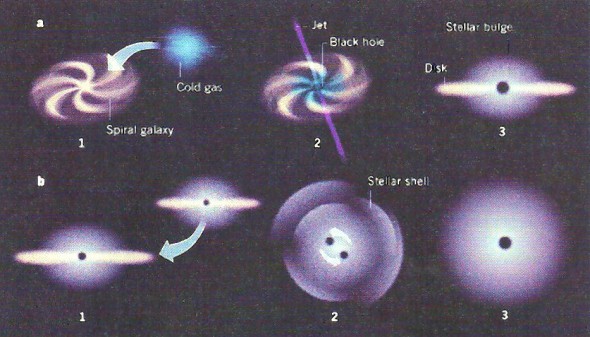
That’s likely to be the form of any major counterpoint to these articles; it’s unlikely there’s an error in the pure mathematics, but frankly quite likely that there’s a problem in the math’s theoretical underpinnings. Note that those problems, if they exist, are problems with physics in general and not with this study in particular; even if roundly discredited by further research, this paper will have directed and motivated that very discrediting research, and thus pushed a major area of physics forward. That’s science for you — it’s very possible that by attacking Big Bang dogma, this paper could help to prove it.
Source: GEEK













 © 2024
© 2024
0 comments